6 min
0
10.04.2022

People who say nothing in life is perfect have forgotten about perfect squares. Perfect squares are a special subset of numbers that have some very unique properties. These properties form a basis for various factorization techniques that are useful in simplifying more complicated mathematical problems, such as completing the square in quadratic equations. Furthermore, understanding the nature of perfect squares can help you to see special relationships between numbers.
What Is a Perfect Square Number?
Perfect squares are defined as a number from the natural number set N that can be expressed as a product of some other integer number and itself. The product of two equal integers can be expressed as an exponent (also known as an index or power) of 2 with the integer number as the base number. This number is also known as the square root of the perfect square number. Square rooting a number is the inverse function of squaring a number.
In other words: if a positive whole number has a square root that is also a whole number, then it is known as a perfect square. If the square root is a decimal, then it is not a perfect square. The square root must be a rational number.
The formal mathematical definition is as follows:
Definition: Let a∈Z, then there exists a perfect square number n such that n=a×a = a2 for all n∈N. The integer a is known as the square root of n.
Note: Since the integer set Z is closed under multiplication, any product of two numbers belonging to Z also belongs to Z. As N is a subset of Z, this property holds.
A perfect square n is always a positive integer, but its square root a can be a positive or a negative integer.
For simplicity, we shall only discuss perfect squares from products of positive integers – also known as the subset of natural numbers N. Therefore, a∈ N is assumed.
Properties of Perfect Square Numbers
Positive integer square numbers of any size all have certain things in common. These commonalities are called properties. Here are some important properties of perfect square numbers:
- The last digit is 0, 1, 4, 5, 6, or 9.
- The digital root is always 1, 4, 7, 9.
- If the last digit is 6, then the penultimate digit must be odd.
- If the last digit is not 6, then the penultimate digit is even.
- If the last digit is 5, then the penultimate digit must be 2.
- If the last digit is zero, it must also end in an even number of zeros.
- Even square numbers have an even square root. Odd squares have an odd square root.
- The remainder after dividing by 3 is either 1 or 0.
- The remainder after dividing by 4 is either 1 or 0.
- They always have an odd number of prime factors.
There are many other properties, recursive formulas, and nth term generating formulas for square numbers.
How to Identify a Perfect Square
There are many ways to identify if a number is NOT a perfect square, all of which use the properties listed above. If a number does not have all the applicable properties, it cannot be a perfect square, and thus, the process ends there.
Example 1: 732, 2747, 3928, and 19253 are not perfect squares.
Example 2: the digital root of 3857 =3 + 8 + 5 + 7 = 23, 2 + 3 = 5. Therefore, 3857 is not a perfect square.
However, if a number does have some properties, it does not necessarily imply it is a perfect square – only that it MIGHT be one. For example, the digital root of 22 is 4, but 22 is not a square number. Also, the number ends in 2, which automatically eliminates it as a square number.
Once you have found a possible perfect square, you may proceed with your investigation further by finding the integer square root. This is the main method of identifying a perfect square. Proving that a number has an integer square root would imply that the number is a perfect square. The simplest and most effective algorithm to finding the square root of a number only takes five steps! These are as follows:
- When given a number n, group the last two digits of n as a pair. Leave the other numbers as a separate group.
- Note that the last digit of n can tell us what the last digit of the square root a will possibly be. It is the single-digit square root of a perfect square that also has the same last digit. You will get two possible numbers.
- Find the perfect square closest to but smaller than the group made from the numbers, excluding the pair. Note the square root of it. This will be a digit in the square root a in the position next to the last digit determined in the next steps.
- Multiply the square root found in step 3 by 1 more than the square root.
- If the number found in step 4 is larger than the group of numbers, you should choose the smaller of the two numbers found in step 2 as the last digit of a. If it is smaller, then choose the larger of the two numbers in step 2.
Combining your answers, you will get the integer square root.
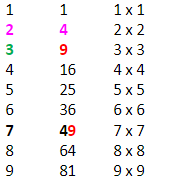
Example 1: Let a = √529. Find a.
Step 1: √529 = √5 29
Step 2: Since the last digit is 9, the possible last digit of the square root of 529 is 3 or 7.
Step 3: The perfect square closest to but smaller than the value of 5 is 4. The square root of 4 is 2. Therefore, 2 is the first digit of the square root a.
Step 4: Since the square root found in step 3 was 2, and 2+1 = 3, then 2 x 3 = 6.
Step 5: As 6 > 5, we choose 3 and not 7 as the last digit of a.
Therefore, a = √529 = 23
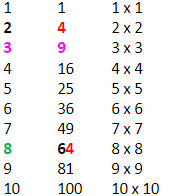
Example 2: Let a = √1444. Find a.
Step 1: √1444 = √14 44
Step 2: Since the last digit is 4, the possible last digit of the square root of √1444 is 2 or 8.
Step 3: The perfect square closest to but smaller than the value of 14 is 9. The square root of 9 is 3. Therefore, 3 is the first digit of the square root a.
Step 4: Since the square root found in step 3 was 3, and 3+1 = 4, then 3 x 4 = 12.
Step 5: As 12
Therefore, a = √1444 = 38
There are other methods involving factoring surds or prime factorization that can help you to find square roots. Always check answers with a calculator!
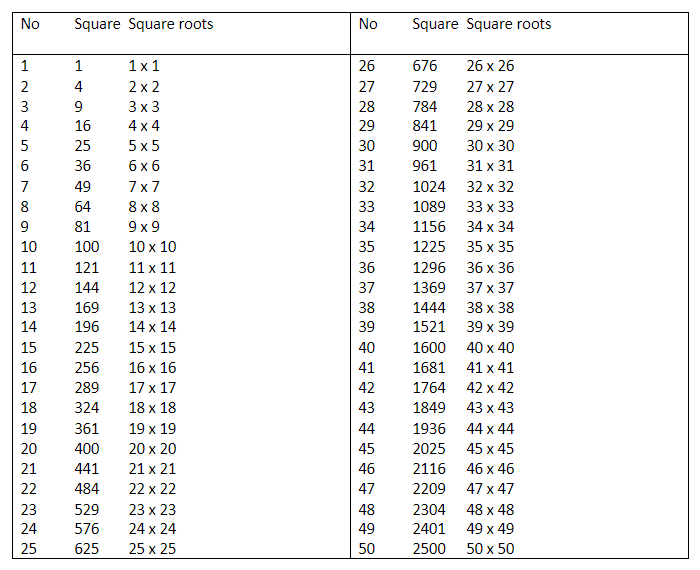
List of Perfect Squares
The following numbers are a list of the first 50 integer square numbers:
Summary
Perfect squares are a set of numbers that have interesting properties and are the foundations of understanding wider concepts in algebra and calculus. Exploring the special relationships between different sets of numbers is a fascinating journey and, unsurprisingly, a fundamental branch of mathematics with various implications. Getting to grips with perfect squares is just a stepping stone to more interesting mathematical discoveries.
It may be good practice to find an integer square root of a randomly chosen large number. Eliminate numbers by applying the properties as quick checks. Then investigate further these possible perfect squares by seeing if an integer square root exists.
As a thought exercise, try to prove why some of these properties hold for perfect square numbers.



