Acute Scalene Triangle: Definition and Example Tasks

Objects are formed by shapes that you generally discuss in your geometry classes. Take a look at a pyramid, an ice cream cone, a traffic cone, a triangular ruler, and a pizza slice. What do they have in common? That's right! They are all formed from a triangle.

What makes a triangle a triangle? It's defined as a polygon with three line segments that are non-linear and intersect one another. The points where two or more lines or curves meet are called vertices. Close to the vertex are the angles, which are the spaces between two intersecting lines.

Although the real-life objects mentioned above are all triangles, you may notice that they also differ. These objects differ in the length of their respective sides; thus, their angles vary as well. Hence, classifications of triangles depend on the different measures of their angles and the sides of a triangle.

This article will discuss the different classifications of triangles and will focus on acute scalene triangles. Quick questions are placed within each segment to help you assess your knowledge.

Types of Triangles

Types of triangles are determined both in terms of the angle measures and the relative lengths of their sides. They are, namely, Equilateral, Obtuse, Scalene, Acute, Right, and Isosceles.

Right Triangle

The right triangle is composed of only one right angle (90-degree angle). A hypotenuse pertains to the side that is opposite to the right angle. Students apply the Pythagorean theorem to measure the length of the hypotenuse.

Acute Triangle

This kind refers to a triangle with three acute angles (less than 90 degrees). It's often considered the smallest angle.

Obtuse Triangle

This refers to a triangle with one obtuse angle (greater than 90 degrees, but less than 180 degrees). Thus, its interior angles can measure more than 90 degrees. Opposite to the obtuse angle is the longest side of an obtuse triangle.

Scalene Triangle

It is a triangle that contains three sides of different lengths. This means that all three sides of a scalene triangle have different lengths and measures.

Isosceles Triangle

Unlike the prior one, isosceles triangles have at least two sides that have equal measure.

Equilateral Triangle

The equilateral triangle contains three sides of equal length and equal angles. Thus, it's also called the equiangular triangle.

Upon knowing the different classifications of triangles, you can easily identify acute scalene triangles. It mainly depends on the angles of the triangle. What are they, and what are their properties or characteristics?

What Is an Acute Scalene Triangle?

In understanding what an acute scalene triangle is, we must recap the characteristics that make up acute and scalene triangles. As mentioned, an acute triangle consists of three acute angles (measuring less than 90 degrees), while scalene triangles contain three unequal sides and angles.

A theorem states that the angle bisector will always be longer than the altitude of the triangle in the case of scalene triangles.

Acute Scalene Triangles vs. Acute Isosceles Triangle

Acute triangles can also be isosceles - aside from scalene ones. How does an acute scalene triangle differ from an acute isosceles triangle? Again, it is advisable to review the properties that constitute an isosceles.

Compared to acute scalene triangles, acute isosceles triangles also have less than 90 degrees angles. But contrary to acute scalene triangles, the latter has at least two congruent sides. Congruent sides mean the triangle's sides have equal lengths and angles.

How to Identify an Acute Scalene Triangle

It will be easier to recognize an acute scalene triangle if you are aware of its properties. Bearing the characteristics of an acute scalene triangle in mind, you should be able to categorize this type of triangle using a protractor as a tool for measurement.

Measuring Angles Using a Protractor

A protractor is a tool used to measure curves and angles. You can use this tool to measure the angles of a triangle and determine whether it is an acute scalene triangle. Below are easy-to-follow steps to do this:

1. Put the midpoint (middle point) of the protractor on the vertex of the angle.
2. Align the other side to the "zero" line of the protractor.
3. Trace the degrees where the other side crosses the numbers scale in the protractor.
4. Tally all angles and begin identifying whether the triangle is an acute scalene.

It would be an acute scalene triangle if:

• All angles are less than 90 degrees
• All sides are unequal

Tasks Examples with Solutions

Figure 1:

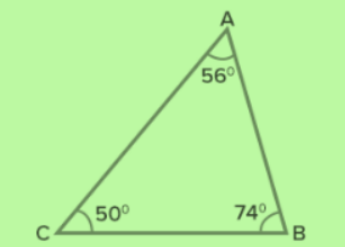
Is Figure 1 an acute scalene triangle?

YES! The triangle has three acute angles and three sides of different lengths.

Figure 2:

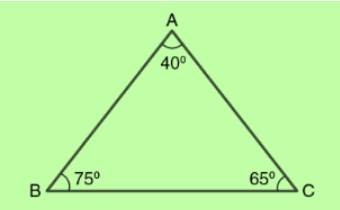
Is Figure 2 an acute scalene triangle?

NO. Although all three angles are acute, there are at least two equal sides (Lines AB and AC). Hence, this figure is an example of an acute isosceles triangle.

The Use of Acute Scalene Triangles

Because of its varying internal angles, one might think that a random drawing of a triangle will likely result in an acute scalene triangle. What is the use of this kind of triangle?

This type is reportedly common in roof trusses and other modern construction.

Summary

In this article, you learned the different classifications of triangles and the definition and properties of acute scalene triangles. You also learned the ways on how to identify whether a triangle is an acute scalene triangle or otherwise.

Applying these learnings in your upcoming geometry classes can help you improve your performance and aptitude for the subject. It is important to familiarize yourself with this topic, as it will be utilized in higher geometry courses and problem-solving tasks that require proving.