
4 min
0
10.04.2022

The process of obtaining the derivative of a trigonometric function from a trigonometric identity, or its rate of change with respect to a variable, is known as the differentiation of trigonometric functions. The sine function's derivative is written sin′(a)= cos(a), which means that the rate of change of sin x at a given angle x= an is determined by the cosine of that angle.
By using the quotient technique to functions like tan(x)= sin(x)/cos(x), all derivatives of circular trigonometric functions may be determined from those of sin(x) and cos(x) (x). The derivatives of the inverse trigonometric functions are obtained via implicit differentiation after these derivatives are known.
If you have a tight math homework deadline, read this article and contact us for further assistance!
Derivative of sec x Formula
The product of secant and tangent functions equals the differentiation or derivative of a secant function with respect to a variable. The derivative of the sec x function with respect to x equals the product of sec x, and tan x is the derivative formula.
Assuming x is a variable, the secant function is stated in trigonometric mathematical notation.
d/dx(secx) = secxtanx
The differentiation of a sec x function with respect to x may be represented d/dx(sec x) in mathematics or as (sec x)'.
Other Form
The derivative of the secant function can be expressed in terms of any variable.
- d/dh(sec h) = sec h tan h
- d/dw(sec w) = sec w tan w
- d/dy(sec y) = sec y tan y
Proof of Derivative of sec x
The product of the secant and tangent functions is the derivative of a secant function with respect to a variable. If 'x' is used to represent a variable, the secant function is expressed as 'sec x' in mathematical notation. The product of 'sec x' and 'tan x' is the differentiation of 'sec x' with regard to 'x'. In differential calculus, the derivative of a secant function is determined using the first principle of differentiation.
Function Differentiation in Limit Form
First, according to the definition of the derivative, write the derivative of a function in terms of limits operation form.
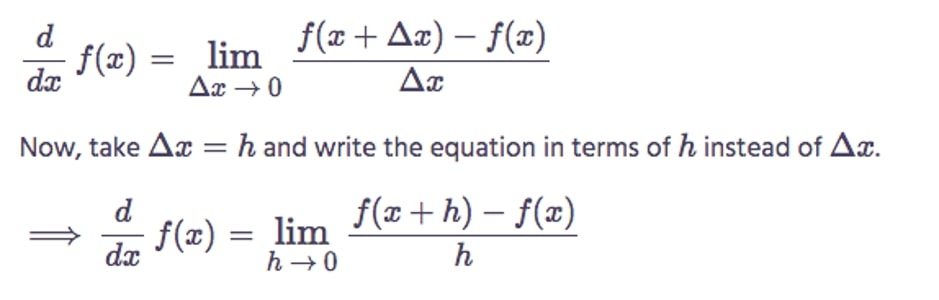
If f(x) = sec x, then f(x+h) = sec(x+h).
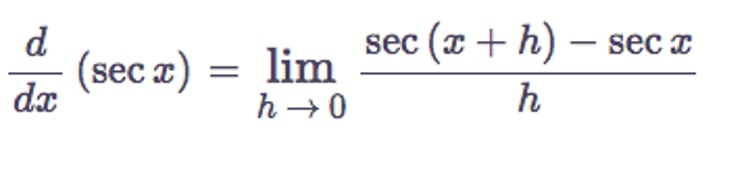
Ways of Calculating
Quotient Rule: The Quotient Rule is a technique for obtaining a function's derivative (differentiation) in the form of the ratio of two differentiable functions in Calculus. It is a formal rule for dividing one function by the other function in differentiation situations.
The quotient rule is based on the notion of the derivative limit. The quotient rule starts with the lowest function and concludes with the lowest function squared.
Chain Rule
The chain rule explains how to calculate a composite function's derivative.
d/dx[f(g(x))]=f′(g(x))g′(x)
It might be helpful to view the functions f and g as 'layers of a problem.' The chain rule advises us to differentiate the outer layer first, leaving the inner layer intact (the term f'( g(x))), and then differentiate the inner layer (the term g'(x)).
Product Rule
The Product Rule teaches us how to discern the difference between expressions that are the product of two simpler expressions:
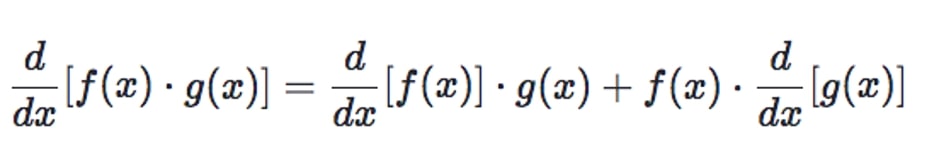
Similarly, there is a derivative of tan x, a derivative of csc x, and more in the subject of trigonometry. For a better understanding, you can ask for online assistance in your homework.
For help in researching a paper, you can also contact Studybay.



