
8 min
0
10.04.2022

Calculating the volume of a square Pyramid is a geometry problem often found in math homework and exams. They are solved using a practical application of algebra.
In this article, we shall learn definitions relating to square pyramids, the formula for the volume of the square pyramid, and show how to use formulas to solve for the volume of any pyramid through worked examples.
The Formula for the Volume of a Square Pyramid
The formula for the volume of a square pyramid V is:
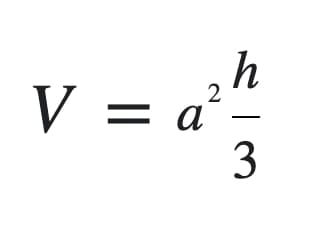
where a is the side length of the base and h is the perpendicular distance from the base to the apex, also known as the perpendicular height of the pyramid.
Note that a2 is also the area of a square with side length a. Therefore, part of the calculation will require you to find the area of the base, which is measured in square units. Hence, the formula can also be written as:
V = ⅓ Bh
where the base
b = a2
In fact, the generalized formula is
Volume of a square pyramid V = 1/3 x base x height
This formula can be used to find the volume of any pyramid with a polygon base as long as you are able to calculate the area of the base, provided that the height h is the perpendicular distance from the apex to the plane containing the base.
The height h can be calculated in various ways by choosing specific trigonometric formulas depending on what values are known.
The volume V calculated using the formula will be measured in cubic units.
The unit is determined by the unit measurement of each variable involved in the calculation, that is, a and h. Both of these variables need to be measured in, or converted to, the same units before being used in the formula.
Examples of How to Calculate the Volume of a Square Pyramid
Many different questions could be asked regarding the volume of a square-based pyramid. Typically, exam questions will ask you to find an unknown variable needed for the volume formula using some known values. Here are some examples using the same square-based pyramid for a better understanding.
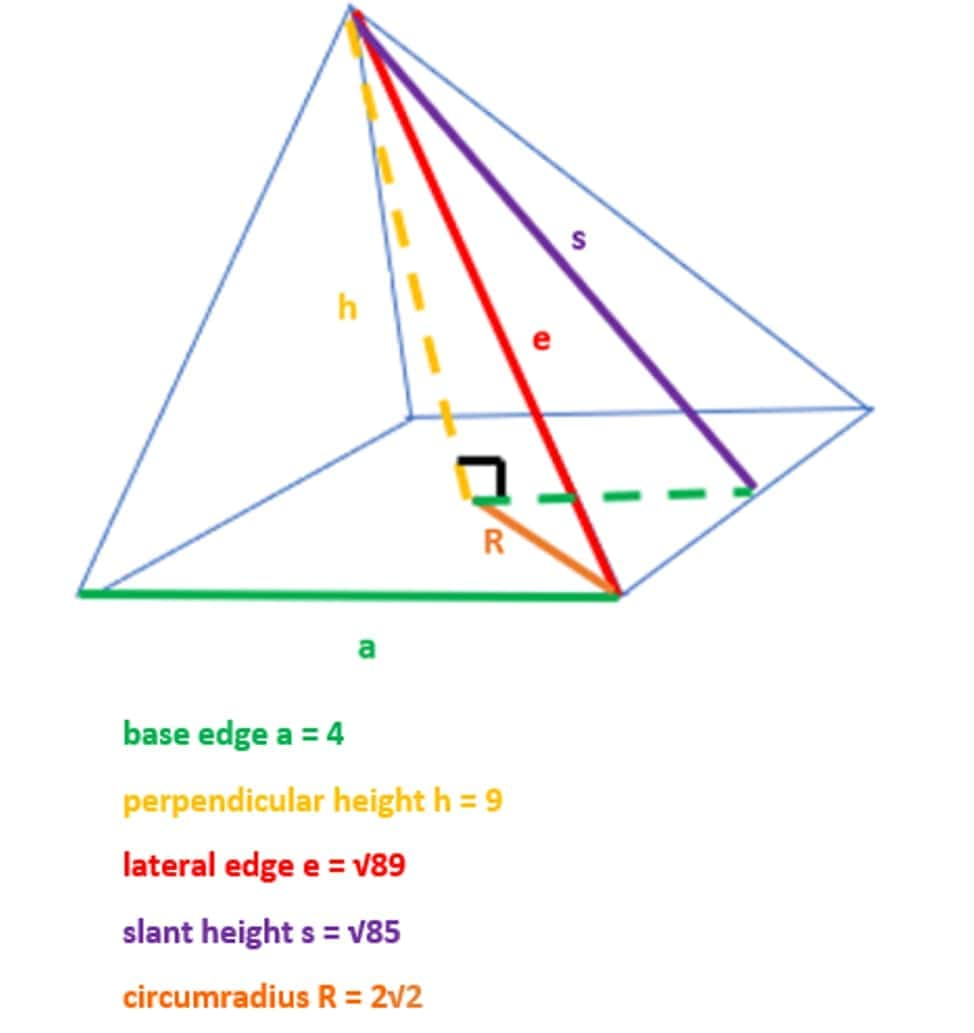
Example 1: Finding the Volume when the height of a pyramid and the length of the base is known.
This is the simplest problem you will come across since all variables needed are given. Substitute the values of a and h directly into the formula.
V = ⅓ x 42 x 9 = 48 m3
where m3 is the unit measurement and represents cubic meters. This is because the area of the square base is 4m x 4m = 16 m3 or 16 square meters. This value is multiplied by the height, which is 9 meters. Hence we have a product of three-meter values: m x m x m = m3.
Example 2: Finding the Volume when the height of the pyramid is unknown, but the base and the lateral edge length is known.
The lateral edge length is the length measured along the edge of a lateral face, which connects the apex to any vertex of the square base. In other words, it is the longest side on an isosceles triangle face. This edge is typically denoted by e.
Here, you are given a = 4, e = √89.
To find the volume of the pyramid, you must first find the height h. In this scenario, there are a few ways you could approach this problem. All ways involve using the Pythagorean theorem and finding the area of a triangle. You may even use trigonometry.
One way is to apply the Pythagorean theorem twice. First, form a right triangle using e as the hypotenuse, and the bottom side a/2, half the length of the base. We can use this triangle to find the slant height of the pyramid s which is the length between the apex and the base side.
The Pythagorean theorem states:
a2 + b2 = c2
where c is the length of the hypotenuse and a and b are the other two side lengths.
Applying this to find the slant height, we get:
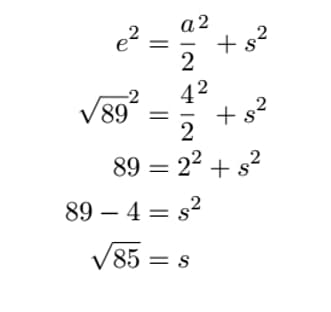
Now we can use our value of s to form a second triangle with s as the hypotenuse, the bottom side a/2, and the final side h. We apply the theorem again and solve for the unknown h.
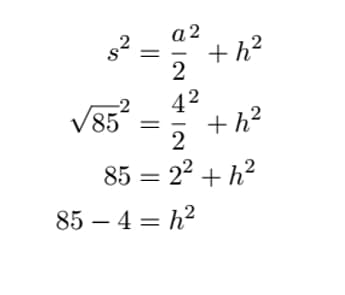
Hence,
h = √81 =9 which we know to be correct. Then the volume is found using the formula just as in example 1.
Exercise: Try finding the height h by:
- Constructing a right triangle to find the circumradius R, which is the length between the base midpoint and a vertex that is not the apex. Trigonometric identities could be used to do this. You should get R = 2√2.
- Constructing a right triangle with bottom side R, hypotenuse e, and the third side h, then solve for h using the Pythagorean theorem.
Example 3: Finding the Volume when the height of the pyramid is unknown, but the base length and the lateral surface area (LSA) is known.
Here we are given a = 4 and the LSA = 8√85
Note that LSA = 4 x area of lateral surface = 4 x ½ x as (area of an isosceles triangle).
From example 2 we know that
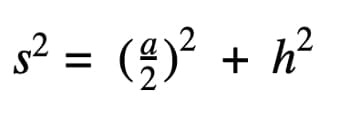
Thus,
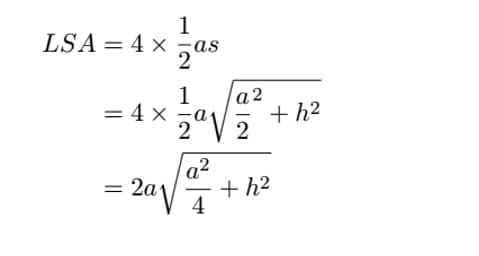
Therefore,
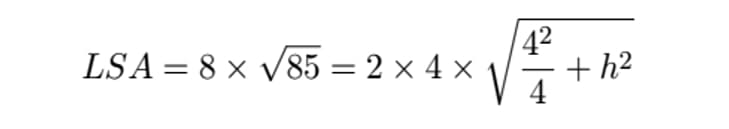
Simplifying, we get:
85 = 4 = h2
Rearranging for h, we get:
h = √81 = 9
Now we again have all the values needed to find the volume and we plug them into the formula as we did in example 1.
How to Calculate the Volume of Other Types of Pyramids
The main types are as follows.
Volume of a Rectangular Pyramid
A Rectangular pyramid is a pyramid with a rectangular base. Since squares are a type of rectangle, all square pyramids are rectangular pyramids. But the converse is not true.
Example:
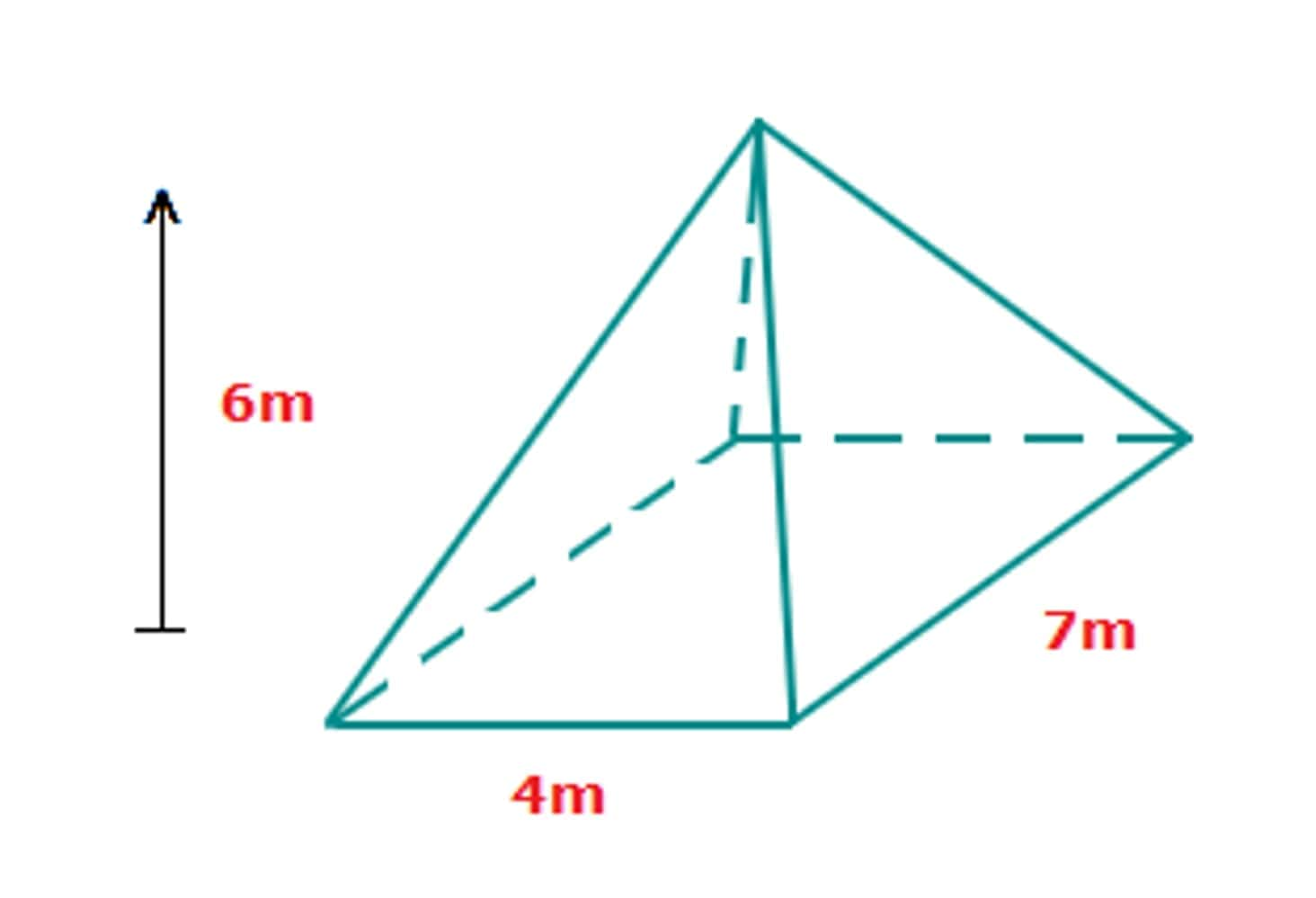
area of the base = 4 x 7 = 28 cm2
V = ⅓ x 28 x 6 = 56 cm2
Volume of a Triangular Pyramid
A triangular pyramid is commonly known as a Tetrahedron. All faces of this pyramid are triangles. Using the generalized formula, you can find the volume.
Example:
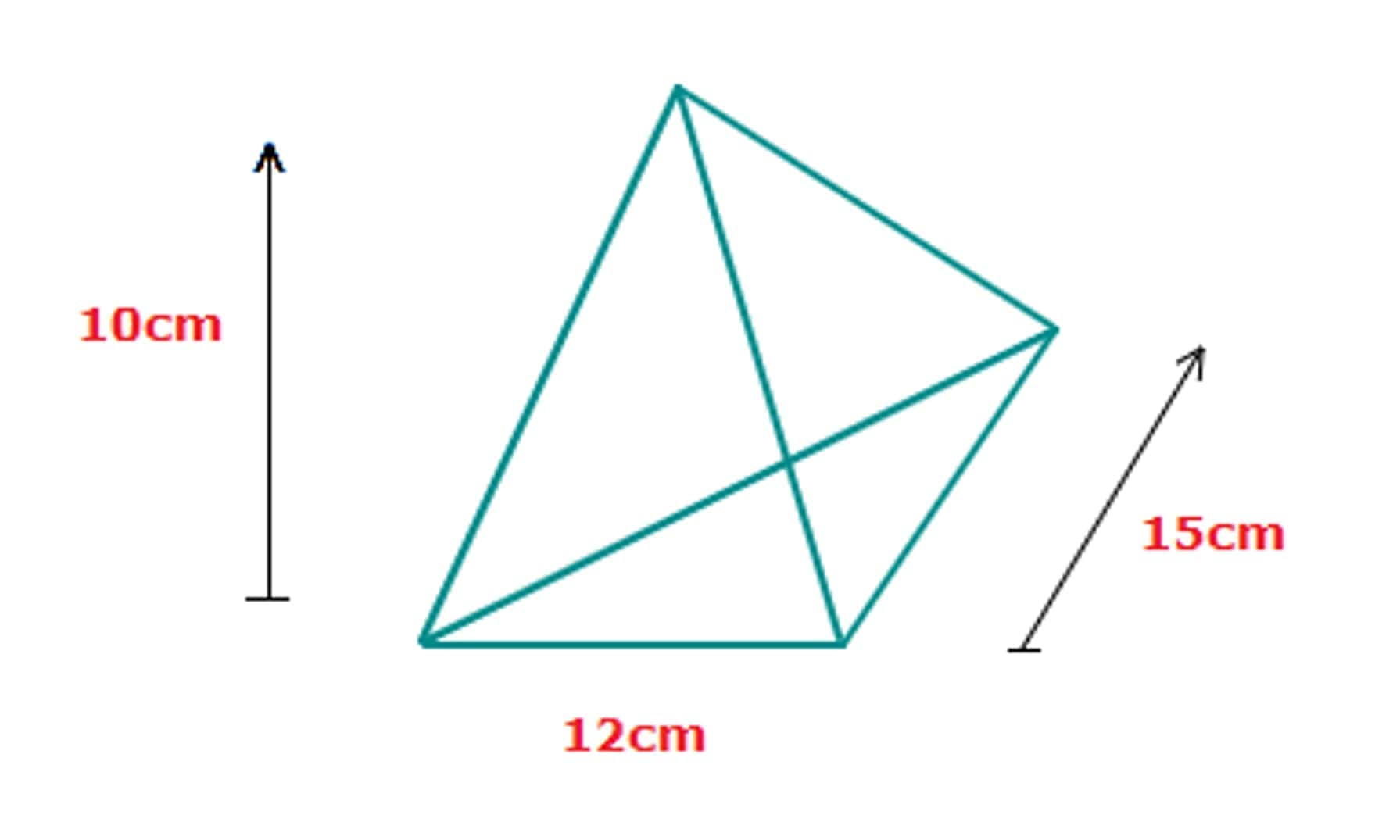
area of the base = ½ x 12 x 15 = 90 cm2
V = ⅓ x 90 x 10 = 300 cm3
Volume of an Oblique Pyramid
An Oblique pyramid is a pyramid where the apex is not directly above the midpoint of the square base. The volume of an Oblique pyramid can be found using the same formula, and the height is the perpendicular distance between the apex and the plane on which the base lies.
Example:
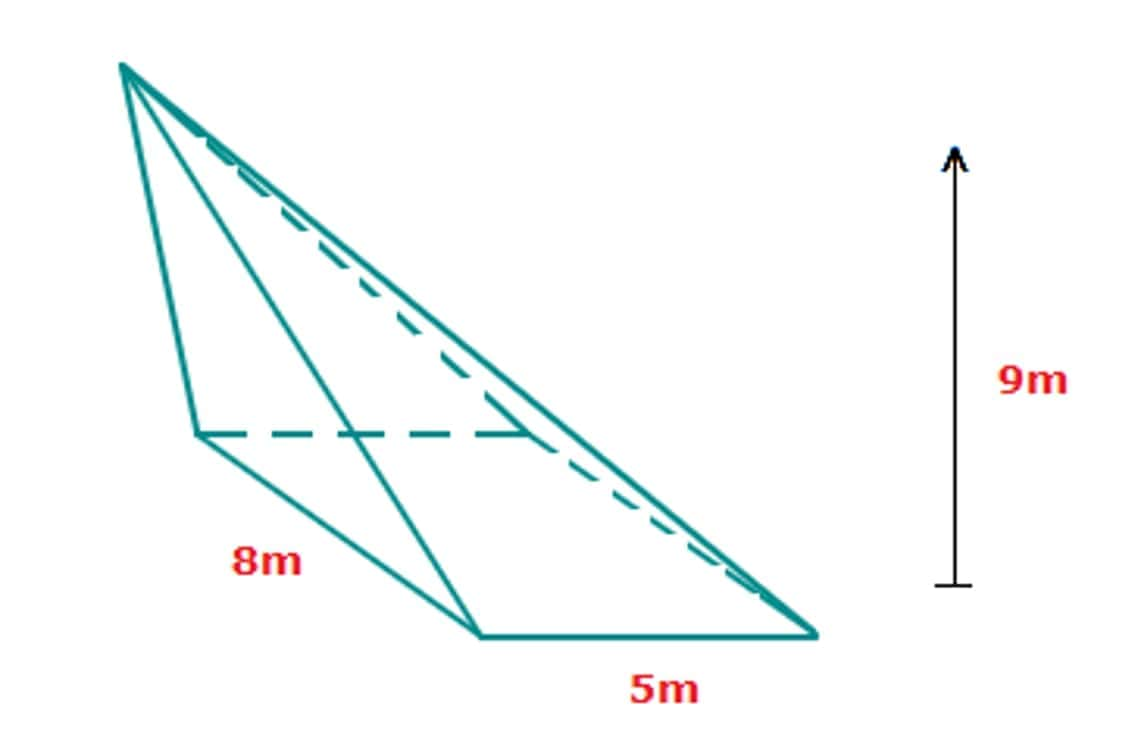
V = ⅓ x 8 x 5 x 9 = 120 m3
What Is A Square Pyramid?
When thinking of pyramids, the first images that should come to mind are the ancient pyramids found in Egypt. In fact, throughout history, many early civilizations around the world built pyramid-shaped structures. This makes pyramids one of the oldest geometric shapes known to man.
A square pyramid is exactly the same shape as the ancient pyramids of Egypt. The base of the pyramid is a square, and the other faces of the square pyramid consist of four congruent isosceles triangles connected to each side of the square base. The top vertex of each isosceles triangle joins at the apex - the highest point on the pyramid.
A lateral surface of a shape is any face that is not the top or base of a shape. Thus, each isosceles triangle face is a lateral surface.
The apex of a square pyramid is located perpendicularly above the midpoint of the base. This means that a square pyramid is a Right Pyramid by definition.
If all faces were congruent equilateral triangles instead of isosceles triangles, then the shape formed would be called an equilateral square pyramid. In this case, the length of all edges would be equal.
The square pyramid belongs to a bigger class of pyramids known as the regular pyramid. Regular pyramids are any right pyramids with a regular polygon base.
Polyhedrons are a class of shapes with a polygon base and triangular sides. Thus by definition, all pyramids are polyhedrons.
The number of triangular faces of a given pyramid will always be equal to the number of sides the polygon base possesses. However, they do not necessarily have to be congruent when the base is an irregular polygon.
Conclusion
Note that not all possible exam questions were shown in the examples. Similar questions may also arise where other unknowns are needed to be found first before using the formula for the volume. There are many variations of questions linked to pyramid volume that could be asked during an exam, so the invaluable help with your geometry and algebra homework is key. Get professional math homework help!



