
8 min
0
10.04.2022

In mathematics, an incredibly useful value to calculate is the slope of a line. The slope of a line gives us a lot of important information, and its interpretation has many implications in various branches of mathematics. To calculate the slope, you may need to brush up on your algebra and geometry. If you are confident in your knowledge of both, you may continue reading!
Definition of a Slope
To understand the slope of a line, you must first understand what a line really is.
By definition, a straight line is the shortest distance between two points. But when a line is drawn to connect multiple points plotted on a coordinate plane with an x-y axis, it then represents a relationship between the variables x and y and is known as a linear function. A straight line will have a constant gradient between any two points that lie on the same line no matter where they are located.
The slope of a line is a measure of steepness from the horizontal plane. It is also often referred to as the gradient of a line or the angular coefficient of a line as it can be viewed as the angular incline from the horizontal plane or axis.
The slope is an important value to calculate because it tells us the rate of change between the two variables. The larger the value, the steeper the slope and hence the faster the rate of change. The converse is also true.
Conceptually, the slope is referred to as rise over run and can help you to remember which variable is the numerator and which is the denominator in this quotient. The "rise" describes how much the linear function goes up (or down), and the "run" describes how much the linear function moves across. Measurement of height would indicate the use of the vertical y-axis, whereas measuring movement from left to right (or vice versa) would indicate the use of the x-axis.
Furthermore, there are four values for slopes that give us even more insight into the relationship between x and y by giving us information about the direction of a line and graphical placements. These are:
- Positive slope – indicates that we have an increasing linear function, and y increases as x increases. Graphically, we would expect an upward trending line.
- Negative slope – indicates that we have a decreasing function, and y decreases as x increases. Graphically, we would expect a downward trending line.
- Zero slope – indicates a horizontal line, and y remains constant regardless of the value of x. An example of a line with zero gradient is y=0, which is also the x-axis. In fact, any line parallel to the x-axis will have a zero gradient.
- Undefined slope – indicates a vertical line, and the value of x is constant regardless of the value of y. An example of a line with an undefined gradient is x=0, which is also the y-axis. In fact, any line parallel to the y-axis will have an undefined gradient.
Note that the slope is not always a whole number.
General Equations for a Straight Line
There are three main general equations for a straight line, and each form can be more useful than the others depending on the problem at hand.

This equation is known as the slope-intercept form of a straight line.
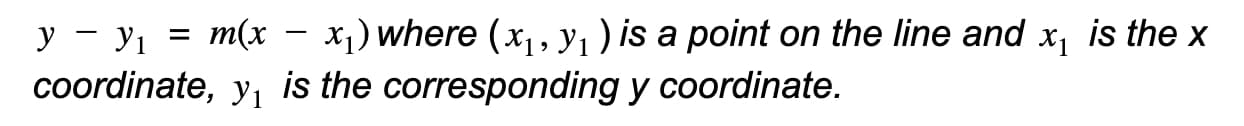
This equation is known as the point-slope form of a straight line.
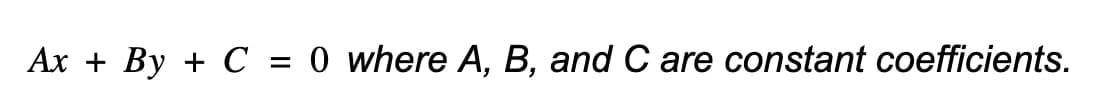
This equation is known as the standard form of a straight line.
The slope in both the first and second equations is denoted by
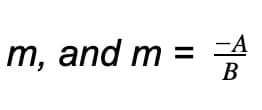
in the third equation. Note that the slope is always the coefficient of x in a linear equation after it is rearranged for y.
Slope Formula
The slope formula is easily derived from intuition and understanding of the slope definition. Since we have established the slope to be the rate of change between two variables, namely x and y, we are examining the vertical distance gained from the horizontal distance moved.
From the point-slope form equation, it can be deduced that:

This is the general formula for finding the slope, provided you are given or can find two points on the line. Since the slope is constant between any two points on a line, we only need one fixed point. The second point is arbitrary and can be anywhere on the line. The ratio will remain the same whichever point we choose for the second point.
Graphing this concept can help to make things clearer.
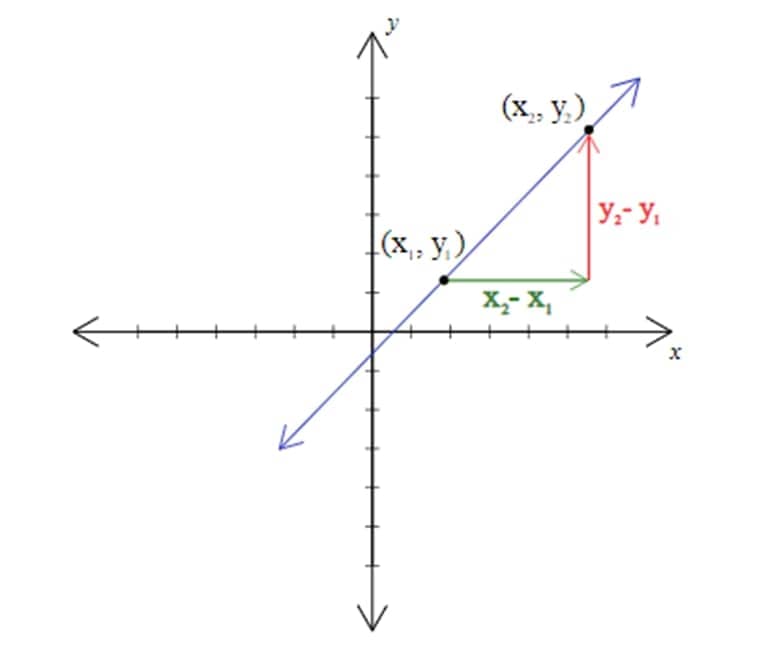
In figure 1, two distinct points are chosen on the line with coordinates (x1,y1) and (x2,y2) and are distinguished by subscripts. The change in x is found by subtraction of the first point's x-coordinate x1 from the second point's x-coordinate x2. Similarly, the change in y is found by subtracting the first point's y-coordinate y1 from the second point's y-coordinate y2.
Hence
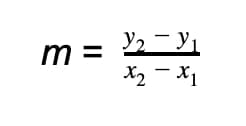
Note: a slope is undefined when the denominator (change in x) is zero, which happens when x1 = x2.
Some Useful Properties
Let L1 and L2 be two lines with slopes m1 and m2, respectively. Then:
- L1 and L2 are perpendicular to each other if and only if m1m2 = -1
- L1 and L2 are parallel to each other if and only if m1 = m2
Examples
Example 1: Find the slope of the line that goes through two points (2,5) and (6,8).
This question is a standard one that just requires you to know the slope formula and to plug in the numbers in the right place.
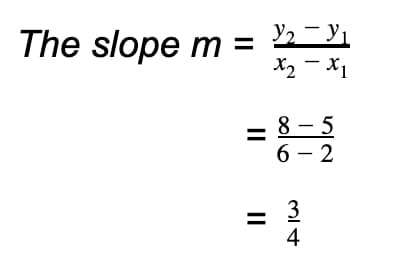
Example 2: An equation of a straight line is 5y + 3x = 9. What is the slope?
The slope of a straight line is always the coefficient of x when the equation of the line is rearranged for y. So:
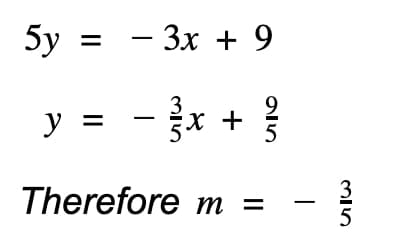
Example 3: The slope given for a line that passes through the points (2,1) and (x,7) is m = 3, find the unknown x-value.
Note that the order in which you subtract your y values and your x values for the given points does not matter, but it does matter that you do it consistently.
Subtracting the second point from the first point:
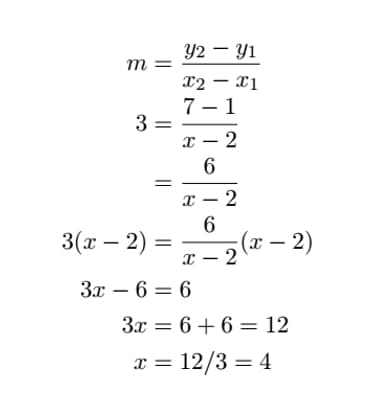
Exercise: Subtract the first point from the second point to solve for x. You should get the same answer because the negative signs that appear in both the numerator and denominator cancel each other out.
Example 4: L1 passes through the points (0,2) and (2,6). L2 passes through the points (3,4) and (5,y). Given that L1 and L2 are parallel, find y. Give an equation of the line L2.
Since L1 and L2, this implies that they have equal slope. Let m1 be the slope for L1 and m2 be the slope for L2. Then:
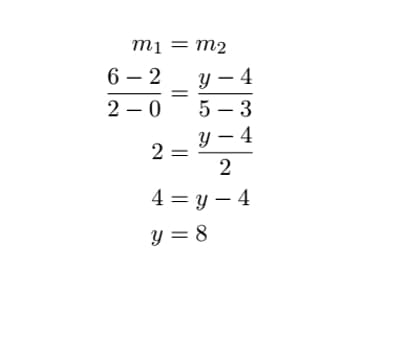
Therefore
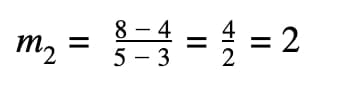
Thus subbing values into the point-slope form
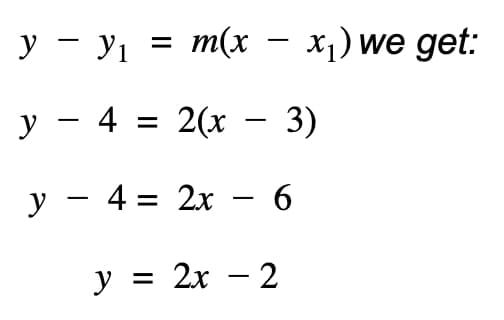
Conclusion
Learning how to calculate the slope of a straight line is an important mathematical skill because it is the stepping stone to understanding the rate of change between two variables. This is essentially the concept behind the fundamental theorem of calculus, also known as differentiation.
If you are serious about maths or have any aspirations in a scientific or finance-related field, then knowing how to analyze linear functions is non-negotiable.
As a general rule, always try to sketch points and lines graphically on a coordinate plane, as it will help you to visualize and solve problems easier. For practice, you can try graphing the lines featured in the examples and see if they turn out as you would expect.
Studybay can help you with your math homework!



