5 min
5
10.04.2022

Geometry students frequently receive assignments that require them to compute the volume, cross-sectional area, or surface area of a rectangular prism. At first glance, this might seem tricky, but it really comes down to a simple formula. In this guide, we’ll explain the concept of rectangular prisms, break down the volume formula, and give real examples.
What Is a Rectangular Prism?
Rectangular prism
Rectangular prism, also known simply as a "prism" or "rectangular cuboid," — is a three-dimensional geometric shape characterized by six rectangular faces, twelve straight edges, and eight vertices (corners).
A rectangular prism must:
- Be a 3-dimensional shape (has height, width, and depth)
- Have polygonal, parallel faces
- Be a hexahedron
- Have parallelogram-shaped sides: this is important and distinguishes a rectangular prism from a triangular prism
- Have 12 edges and 8 vertices
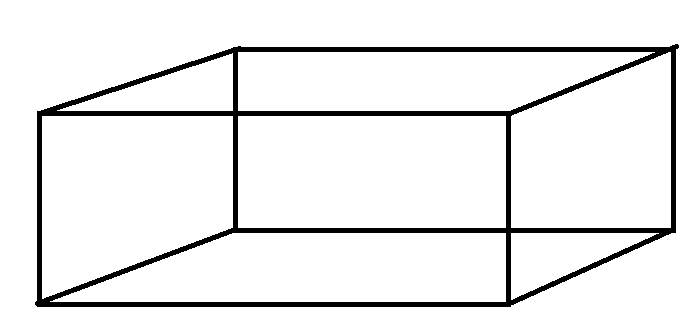
Types of Rectangular Prisms
There are 2 types of rectangular prisms: cuboid and oblique.
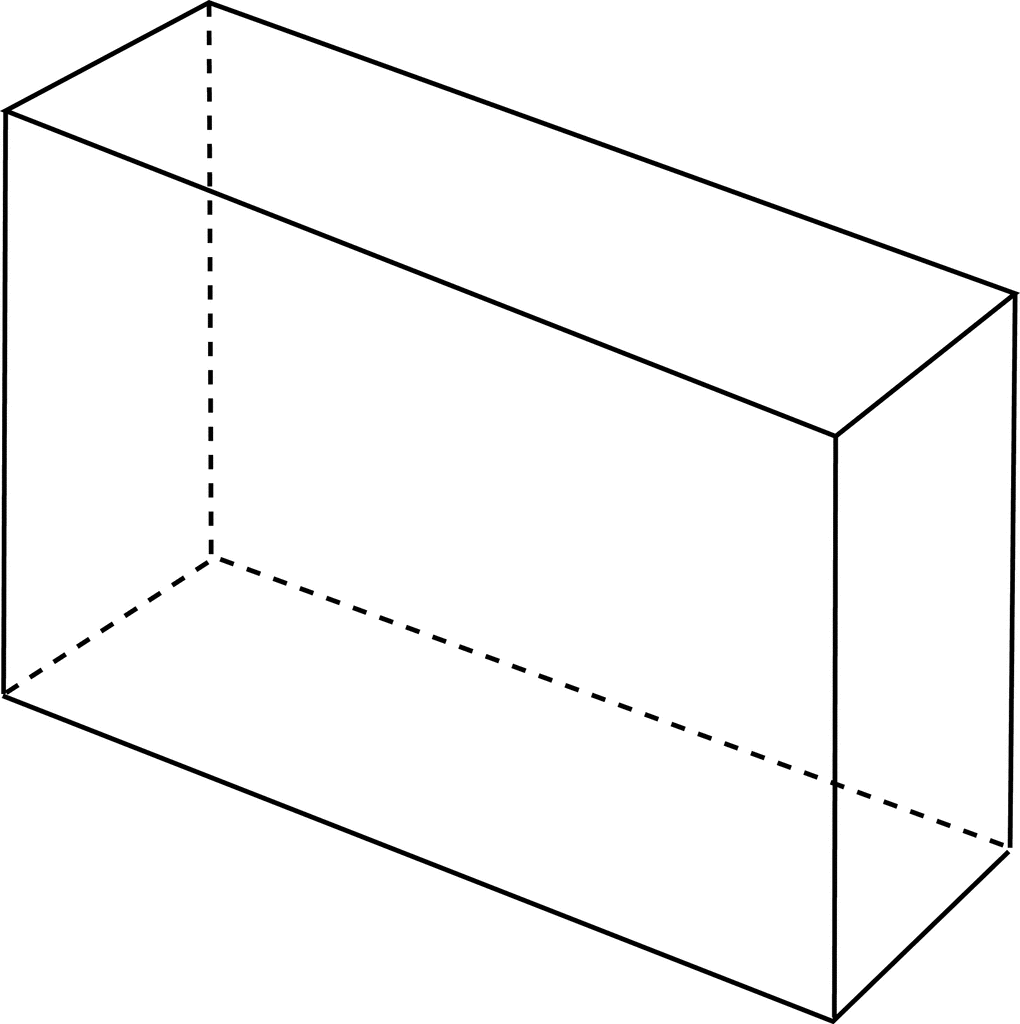
- Cuboid: All of a cuboid’s angles are right angles, and its opposite faces are equal and parallel. This three-dimensional object can also be called a right rectangular prism. Note: cubes are cuboids, but not all cuboids are cubes. Some real-life examples of right rectangular prisms/cuboids include aquariums and refrigerators.
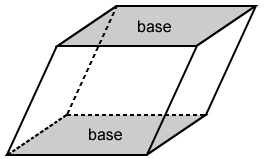
- Oblique rectangular prism: This does not have bases that are perpendicular to its lateral faces.
How to Calculate the Volume of a Rectangular Prism
Finding the volume of a rectangular prism is an incredibly simple task! It’s much easier and quicker than, for instance, finding its total surface area. All you have to do is multiply its 3 dimensions. The formula is as follows:
Volume of rectangular prism = length x width x height
Be sure to express your answer in cubic units; otherwise, it might be marked wrong.
Now, here’s a special case: what if you only know the area of the base and the height of the prism? Guess what! You can also solve the volume problem with this formula:
Volume = area of the base x height
Why does this work? Well, the faces are parallelograms, and a parallelogram’s area = length x width. Thus, if your worksheet provides the rectangular prism’s area of base and height, you automatically know its length and width as well.
Rectangular Prism Calculator
Tasks Examples with Solution
Example #1
Now that you know the formula for finding the volume of a rectangular prism, let’s work through a basic example:
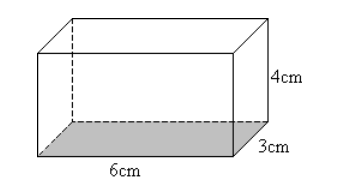
We can see that the height of this prism is 4 cm, the width is 3 cm, and the length is 6 cm. Now, just plug those numbers into the formula! Step-by-step, here’s what to do:
Volume of = length x width x height
Volume of = 6 cm x 3 cm x 4 cm
Volume of = 72 cm3
Remember to express your answer in cubic units (that little three in front of cm). Because the volume of any object is measured in three dimensions, it will always be expressed this way.
Example #2
Let’s try another example! Some worksheets show rectangular prisms as their actual cubic units, as seen in the picture below:
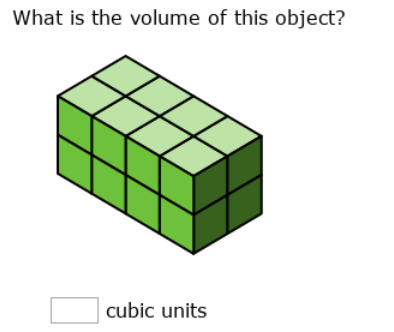
So, first count the cubes in the length: 4. Next, width: 2. Lastly, height: 2.
Multiply them!
Volume = 4 cubic units x 2 cubic units x 2 cubic units
Volume = 16 cubic units
Note: When we are measuring like this, there’s no need to put the little 3. Saying 16 cubic units3 is equivalent to saying 4,096 cubic units, which is definitely the wrong answer!
Summary
As you can see, solving the volume of a rectangular prism is extremely simple. It doesn’t matter if the prism is oblique or cuboid: all you need to do is remember the formula V = l x w x h, and just plug the numbers in. Finding the surface area of a rectangular prism would be a little more complex, but barely – we can cover that in another guide.
If you have any questions about finding the volume of a rectangular prism, leave a comment! Stay tuned for other helpful guides from StudyBay!