
8 min
0
10.04.2022

In the modern world, mathematics is used everywhere, even despite technological progress. That is why educational institutions are so insistently forcing students to study this science. High school students experience the most difficulties because they have to build graphing, find a degree of the numerator or a degree of the denominator, and many other complex tasks. Today we want to pay attention to the rules of horizontal asymptote - with these leading terms, students have the most questions.
Asymptote - What Mathematical Concept Is It?
If you first plot the asymptotes of the curve, then in many cases, the construction of the graph of the function is more straightforward. The fate of the asymptote is full of tragedy. Imagine what it is like all your life to move in a straight line towards the cherished goal, to come as close to it as possible, but never reach it. So it is with the asymptote: it constantly seeks to reach the curve graph of a function, approaches it at the minimum possible distance, but never touches it.
Scientific definition: Asymptotes are straight lines of unlimited length that approach the function you created as close as possible but do not touch it. At the same time, the variable tends to plus infinity or negative infinity. There are such varieties of asymptotes: vertical, oblique, and horizontal.
First Type: Vertical Asymptote
The vertical line x = a is the vertical asymptote of the graph of a function if the point x = a is a breakpoint of the second kind. It follows from the definition that the straight line x = a is the vertical asymptote of the graph of the function f (x) if at least one of the conditions is satisfied:
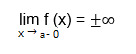
-
the limit of the function with the value of the argument tending to some value "a" on the far left is equal to plus or minus infinity;
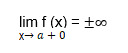
- the limit of the function with the value of the argument tending to some value of "a" from the right is equal to plus or minus infinity.
You can search for the vertical asymptotes of the function's graph at the points of discontinuity and the boundaries of the domain of definition. The graph of a function that is continuous on the whole number line has no vertical asymptotes.
Second Type: Oblique Asymptote
The vertical asymptote, which we described above, is always parallel to the coordinate axes. Therefore, to construct it, we only need a certain number - a point on the x-axis or ordinates through which the asymptote passes. For the slant asymptote, more is required—the angular leading coefficient k, which shows the slope of the line. The x-intercept shows how much the line is above or below the origin.
Thus, the graph of a function cannot contain three or more oblique asymptotes in any way - only two. Otherwise, you performed incorrect calculations. When the graph approaches a single oblique asymptote, it is customary to combine infinities under a single record. It would help if you had the following equation of the oblique asymptote:
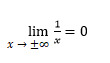
Third Type: Horizontal Asymptote
The first thing to know about the horizontal asymptotes is that they are parallel to the Ox axis. If we have a function like this:
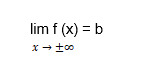
Then y = b is the horizontal line of the curve line y = f (x). The horizontal asymptote is a particular case of an oblique one at k = 0. We will go over horizontal asymptote in more detail since it is most often found in geometry homework.
Asymptote Rules
Finding the asymptotes of the graph of a function is based on the following rules:
- Theorem 1. Let the function y = x be defined at least in some semi-neighborhood of the point x = a, and at least one of its one-sided limits at this point is infinite, that is, equal to + ∞ or - ∞. Then the straight line is the vertical asymptote of the graph of the function. Thus, the vertical asymptotes of the function's graph should be sought at the points of discontinuity of the function. Or the ends of its domain of definition.
-
Theorem 2. Let the function y = f (x) is defined for the argument values large enough in absolute value, and there is a finite limit of the function. The straight line y = b is the horizontal asymptote of the graph of the function y = f (x). It may happen that:
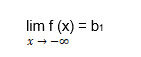 and
and 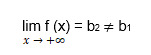 . In given functions, b1 and b2 are finite numbers, and then the graph has two different horizontal asymptotes: left-sided and right-sided. If there are only one of the finite limits, b1 or b2, then the graph has either one left-sided or one right-sided horizontal asymptote.
. In given functions, b1 and b2 are finite numbers, and then the graph has two different horizontal asymptotes: left-sided and right-sided. If there are only one of the finite limits, b1 or b2, then the graph has either one left-sided or one right-sided horizontal asymptote. -
Theorem 3. Let the function y = f (x) be defined for the values of the argument large enough in absolute value, and there are finite limits:
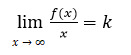 and
and 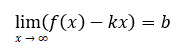 . Then the straight line is the oblique asymptote of the graph of the function. Note that if at least one of the indicated limits is infinite, there is no oblique asymptote. The oblique asymptote, like the horizontal one, can be one-sided.
. Then the straight line is the oblique asymptote of the graph of the function. Note that if at least one of the indicated limits is infinite, there is no oblique asymptote. The oblique asymptote, like the horizontal one, can be one-sided.
How to Find Horizontal Asymptotes?
As we noted above, the horizontal asymptote of a function f (x) is a straight line parallel to the x-axis to which the function f (x) approaches as it tends to infinity. Then we can write the equation of the horizontal asymptote in this form: y = y0, where y0 is some constant (finite number).
To find the horizontal asymptote of the function f (x), you necessary to find y0. You can get the value of y0 by calculating the limits:
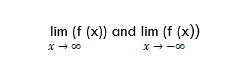
If the value of at least one limit is equal to a finite number y0, then y = y0 is the horizontal asymptote of the function f (x).
Are you having a hard time understanding geometry and formulas? Our paper writing service will help you understand the calculation of degrees of the numerator, degrees of the polynomials, construction of rational expressions for any horizontal asymptote.
Example How to Find Horizontal Asymptotes
There are many geometric assignments associated with finding horizontal asymptote y and x values. We will consider one of these tasks and show the solution algorithm.
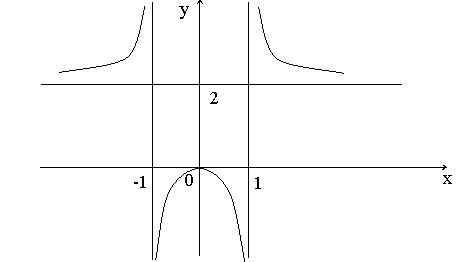
Task: Find all the asymptotes of the graph of a function:
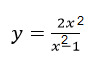
Decision: The function is defined at x є (-∞, -1), U (1, + ∞). Let us find its one-sided limits at the points x = ± 1.
Based on the task, we get the following calculations:
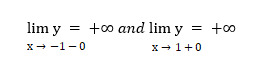
As you can see, we can no longer find two other one-sided limits. The straight lines x = -1 and x = 1 are the vertical asymptotes of the function's graph. Let's calculate:
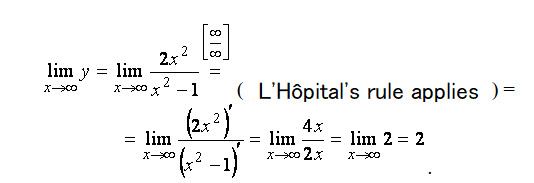
Hence, the straight line is the horizontal asymptote. Since the horizontal asymptote exists, we no longer look for oblique ones (they are not).
Answer: the graph has two vertical asymptotes x = ± 1 and one horizontal asymptote y = 2.
Glossary of Terms You Need When Finding a Horizontal Asymptote
For you to better understand how to solve tasks with the calculation of horizontal asymptote, you need to learn the meanings of such words:
- The number above the fractional bar is called the numerator. The numerator shows how many parts were taken from the whole.
- The number below the fractional bar is called the denominator. The denominator shows how many equal parts the whole is divided into.
- A rational function (also polynomial function) is a function resulting from a finite number of arithmetic operations (addition, multiplication, and division) over the variable x and arbitrary polynomial.
- Exponential growth is multiple multiplications. The more value the function takes, the faster it grows further.
- The graph of a function is a set of points (x; y), where x is the argument, and y is the value of the function corresponding to the given argument.



